2023. 10. 6. 15:52ㆍML, Spatial Computing
⚠ 이 글은 공부용으로 제가 보기 위해 작성한 Vector Calculus (벡터 미적분학) 정리글입니다. ⚠
머신러닝에 필요한 개념들 위주로 정리되어 있어, 미적분학의 전반적인 내용을 공부하고 싶다면 이 글의 내용으로는 부족할 가능성이 매우 높습니다. 권장하지 않습니다.
또한 제가 알아볼 수 있도록 쉽게 정리한 글이니, 오개념이나 수학적으로 잘못된 내용이 있을 수도 있습니다. 저를 너무 믿지 마세요.
댓글로 지적해 주시면 빠르게 수정하겠습니다:)
1️⃣ Derivative: 일변수 (x ~ scalar) 함수에 대한 미분
Derivative(미분)이란 f(x) = y를 만족하는 함수에 대한 그래프에서, x점일 때의 기울기를 의미한다.
일반적으로 f(x) 위에 있는 h가 x로 가까워져 갈 때의, y축 변화량(f(x+h)-f(x)) 나누기 x축 변화량(h)으로 미분값을 정의한다.
고등학교 때 이미 배운 내용이니까 몇몇 주요 규칙에 대해서만 다시 리마인드 해보고 넘어가 보겠다.
- 곱의 미분 : (앞에 거 미분하고 뒤에꺼 그대로) + (앞에꺼 그대로 뒤에꺼 미분한 거)
- 분수 미분 : 분자와 분모 간 곱의 미분을 밑에꺼의 제곱으로 나눠주기
- 합성함수의 미분 : 겉에꺼 미분 더하기 속에꺼 미분... 쭉쭉쭉 반복되면 그게 바로 Chain Rule이다.



2️⃣ Gradient: 다변수 (x~vector, y~scalar) 함수에 대한 미분
기본적으로 고등학교까지 배웠던 일변수 함수와는 다르게, 머신러닝에서 대부분 들어오는 입력 데이터의 형태는 변수가 여러 개인 vector의 형태다.
이런 경우 사용하는 미분 방식이 편미분(partial differenation)이고, 편미분은 특정 변수 1개만 미지수 취급 / 나머지 변수에 대해서는 상수로 취급하고 미분을 하는 방식이다.
즉, Gradient란 다변수 함수 f를 n개의 변수 각각에 대해 편미분한 scalar값을 vector로 쌓은 것을 의미한다.

오른쪽 예시를 살펴보자.
변수가 x1, x2인 다변수 함수 f를 미분하려고 한다. 편미분을 해줘야 한다.
x1만을 먼저 미지수 취급해서 미분해준 scalar값이 2 x1 x2이고, x2를 미지수 취급해서 미분해준 scalar값이 x1^2 + 1이다.
이를 vector로 쌓아준 값이 최종적으로 다변수 함수 f에 대해 미분한 Gradient값이 된다.
그럼 만약에 다변수 함수와 합성함수가 섞여 있는 형태라고 한다면, 미분의 형태는 어떻게 될지 생각해 볼까?
마찬가지로, 다변수 함수 f를 n개의 합성함수 각각에 대해 편미분한 값과 내부 함수의 미분값을 곱한 scalar값들의 vector로 쌓은 값이 최종 Gradient값이 된다.
말이 어려워서 그렇지, 막상 이해해보면 그리 어렵지는 않은 내용이다.
3️⃣ Jacobian: input값과 output값이 모두 vector인 함수에 대한 미분
이번에는 입력값도 vector이고, 출력값도 vector인 벡터 함수에 대해 미분을 시켜보겠다.
벡터 함수라는 건 조금 더 자세하게 말해서 변수가 여러 개(x1, x2....)인 함수가 여러 개라는 뜻이니까, 미분을 시켜줄 때는 이 각각의 벡터 함수의 Gradient를 구해서 쌓아주기만 하면 된다.
즉, Jacobian은 벡터 함수(변수가 여러 개인 함수) 각각의 Gradinet값을 다시 vector로 쌓은 것을 의미한다.
추가로, 여기서 최종적으로 구해지는 Jacobian의 row 길이는 변수의 수(x1, x2, ..., xn)가 되고, column의 길이는 vector 함수 f의 행의 수(f1, f2, ..., fm)가 된다고 이해하면 되겠다.

4️⃣ Hessian: 다변수 (x~vector, y~scalar) 함수에 대한 2차 미분
2️⃣번 파트에서 배웠던 다변수 함수(x~vector, y~scalar)를 2번 미분하는 것을 Hessian이라고 부른다.
조금 더 자세하게 설명해 보겠다.
다변수 함수에 대해 미분하는 것을 우리는 위에서 Gradient라고 불렀고, 그 결괏값은 vector로 나타났던 것을 기억할 것이다.
이 vector를 다시 미분해 주는 것이 결국은 Hessian인데,
Gradient의 결괏값인 vector를 미분하는 것은 곧 벡터 함수(input과 output이 모두 vector인 함수)를 미분해 주는 것과 같은 뜻이게 되니, 결국은 다변수 함수의 Gradient에 대해 Jacobian을 구하는 것이 Hessian인 것이다.
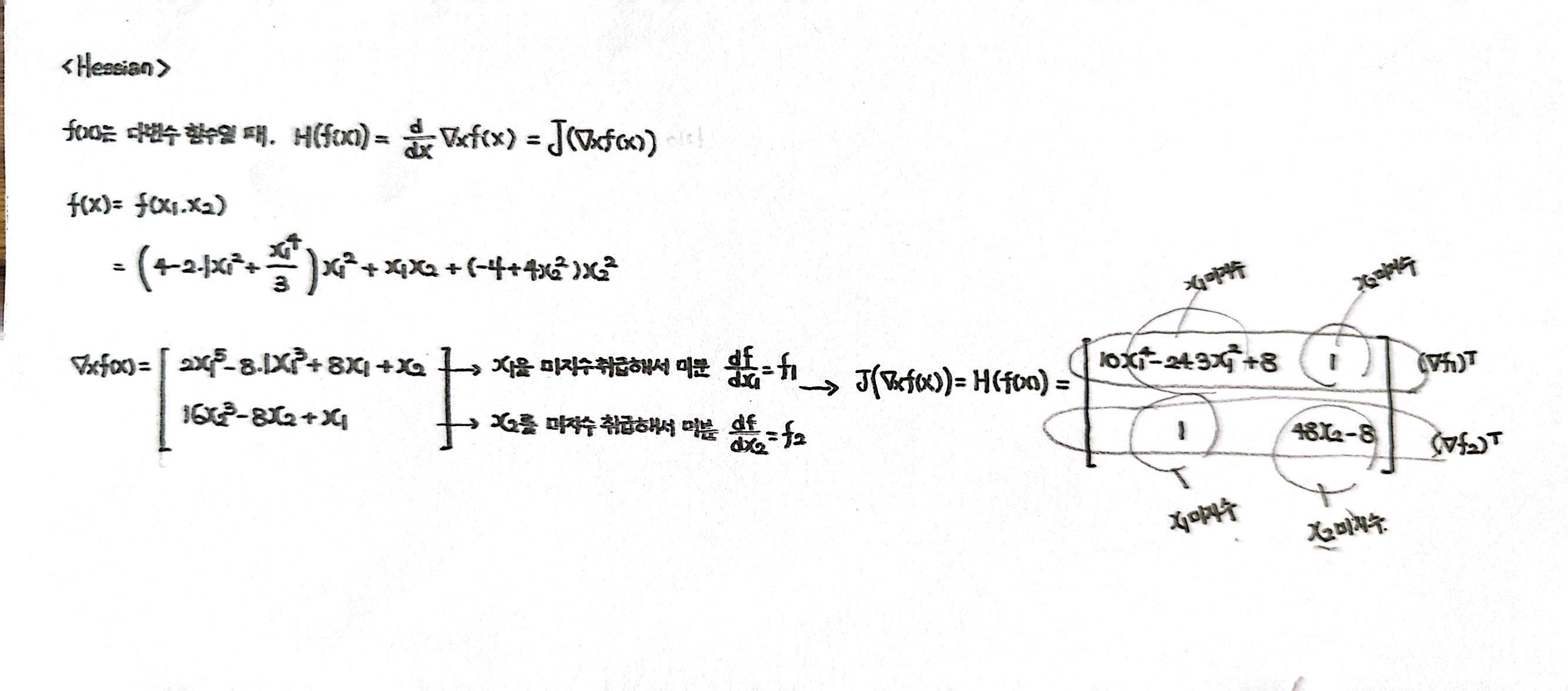
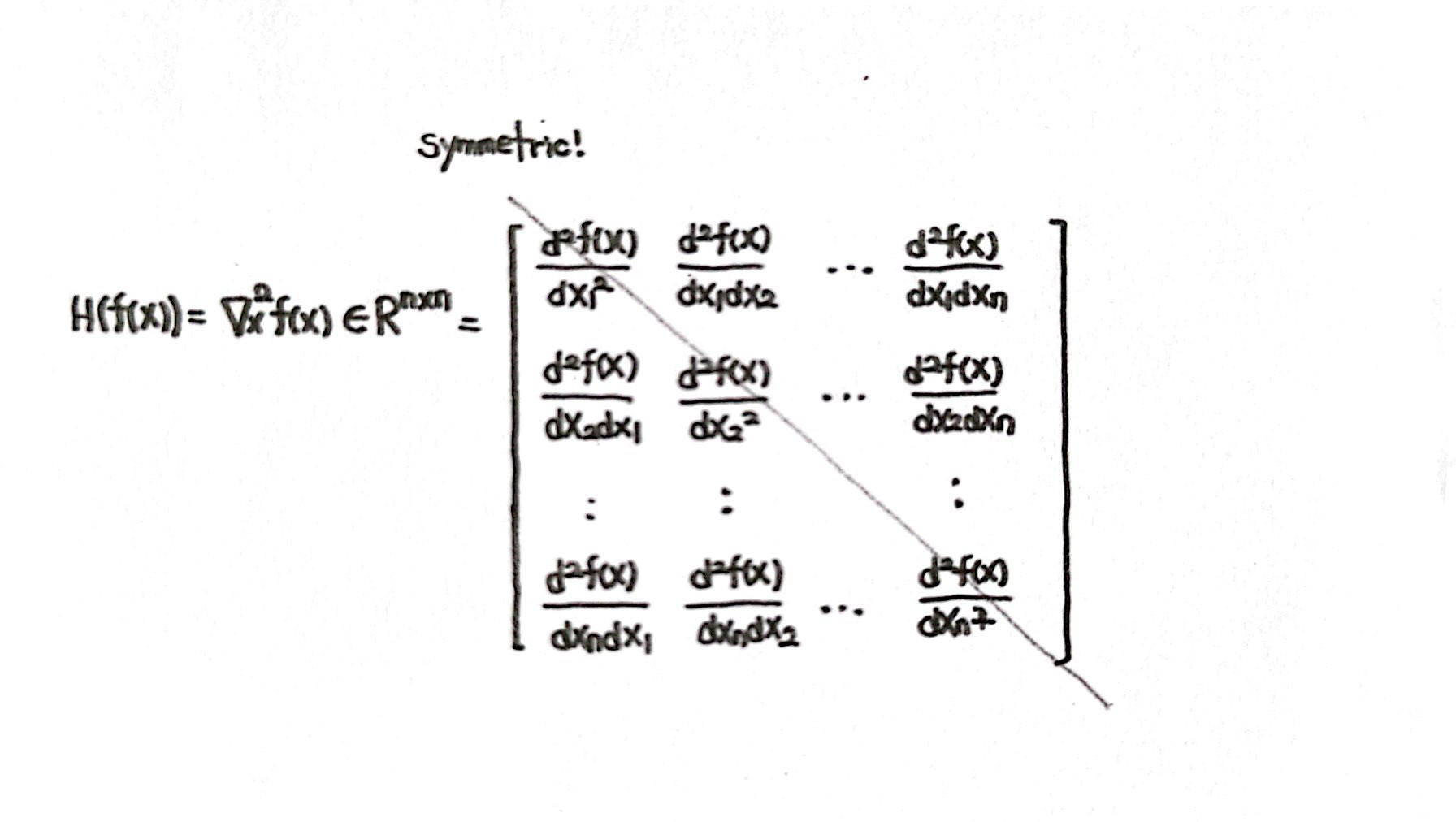
추가적으로, 미분에는 순서가 없다는 성질이 있어
최종적으로 도출되는 Hessian 값은 대각선을 기준으로 대칭인 symmetric 하다는 성질을 가지고 있다는 것까지 알아두도록 하자!
'ML, Spatial Computing' 카테고리의 다른 글
| [Probability and Random Variables] 머신러닝을 위한 확률이론 총정리 (2): Discrete Random Variable Part (1) | 2023.10.18 |
|---|---|
| [ML] 내가 머신러닝 진짜 알기 쉽게 정리해서 올려줄게 (23.10.19.ver) (1) | 2023.10.13 |
| [Probability and Random Variables] 머신러닝을 위한 확률이론 총정리 (1): Probability, Experiment Part (1) | 2023.10.02 |
| [Linear Algebra] 머신러닝을 위한 선형대수 총정리 (上 ) (0) | 2023.10.01 |
| [CoreML] Apple도 AI 한다고 - CoreML의 기본 개념을 배워보자 (0) | 2023.04.14 |
