[ML] 내가 머신러닝 진짜 알기 쉽게 정리해서 올려줄게 (23.10.19.ver)

이번 여름방학 동안에는 <혼자 공부하는 머신러닝+딥러닝> 책을 이용해서 머신러닝의 기초 개념을 공부했었다.

2학기가 시작하면서 "기계 학습" 과목을 수강하고,
코랩과 사이킷런을 이용했던 방식이 아니라, 개념들에 들어있던 수학적인 개념과 원시적인 구현을 하는 방식으로 기계학습을 배우다보니 앞에서는 모르고 넘어갔던 내용이 많았던 것 같았다. (사이킷런의 위대함도 다시금 느끼게 되고)

그래서 이번 시리즈에서는 사이킷런을 통한 머신러닝의 활용보다는, 수학적 지식이 밑바탕이 된 개념적인 이해를 위주로 글을 써볼까 한다.
시험공부 겸, 나중에 내가 리마인드했을 때도 기억이 날 수 있도록.

 

1️⃣ Machine Learnig의 기본 틀(큰 개념)을 먼저 살펴보자.

---

✔️ Machine Learning이란?
: Input Data, x를 넣었을 때, Output Data, y를 예측하는 것
(예시: 주어진 동물 이미지가 개인지 고양이인지? 집의 크기를 가지고 집의 가격은 얼마나 될지 예측하는 문제 등)

이를 수학적으로 설명하면,
집의 크기(x)가 100일 때 집 가격(y)을 100 x w + b로 나타낼 것이고, 여기서의 w와 b는 매개변수라고 부르게 된다는 내용. (어떤 매개변수인지는 밑에서 더 자세하게 보도록 하고, 일단은 이 정도만.)

즉, 머신러닝이란 어떠한 임의의 x값을 입력했을 때, 집 가격 y를 구할 수 있도록 하는 최적의 w와 b값, 즉 최적의 매개변수 값을 찾는 것이라고 볼 수 있다.
최적의 매개변수 값을 찾기 위해 성능을 개선하는 과정을 학습(learning)이라 부르게 될 것이고,
앞으로 우리는 "최적의 매개변수 값을 찾기 위해 성능을 개선하는 다양한 방법들에 대해 배우게 될 것"이다.

✔️ 어떤 방식으로 Machine Learning이 진행되는지 훑어보자!
(집값 예측을 예시로 설명하겠다. 공부를 하면서, 이 큰 틀 안에서 살이 덧붙여지는 방식으로 나중에는 확장될 거다 ^__^)

1. feature vector와 target vector를 담은 training set이 주어지게 된다.
    - feature vector : n개의 입력 데이터가 x = [x1, x2 ..., xn] 이런 형태로 주어질 거다. 보통은 특징(feature, 집의 크기/침실의 개수 같은)이 한 개인 경우는 잘 없으므로 각각의 요소들 역시 (x1 = [x1의 집 크기, x1의 침실 개수 ...] 같은) vector의 형태일 것인데, 이를 feature vector라고 부른다. (벡터는 bold 표시)
    - target vector : y = [y1, y2, ..., yn]의 형태와 같이, 같은 인덱스에 해당하는 x의 feature가 주어졌을 때의 정답값(실제 집값)을 담은 데이터이다. Labeled data라고도 부른다.

2. 파라미터값을 기반으로 예측을 수행한다.
    - 파라미터 값은 처음에는 임의의 값으로 지정해 준다.
    - 파라미터 값(위에서 말했던 w, b에 해당 / Vector 표기로 보면 θ vector)을 앞으로는 가중치(weights)라고도 부르게 된다.

3. 예측한 값과 실제(target, labeled) 값과의 오차를 바탕으로 파라미터값을 update한다.
    - 오차는 쉽게 생각하면 예측값에서 실제값을 뺀 차이일 수도 있고, 보통은 Cost Function, 비용함수 J(θ)를 구해 얻게 된다.
    - 오차가 가장 작은 지점을 찾는 것이 목표이다. (Cost Function J(θ)를 최소로 만드는 θ^를 찾는 것이 목표)
    - 오차가 가장 작은 지점을 찾기 위해 사용하는 방식이 Gradient Descent이다. 
    - J(θ)가 작아지는 방향  Δθ를 미분을 통해 구하는 것이 Gradient이고, 비용 함수가 최소화되는 지점을 그래프의 경사면을 따라 이동한다 해서 붙여진 말이 Gradient Descent이다.

4. 만족할만한 예측 성능이 보일 때까지 2번~3번 과정을 반복한다.

 

2️⃣ Gradient Descent의 원리부터 알아야 Machine Learning을 이해할 수 있다.

---

[Calculus] Gradient Descent를 이해하기 위한 Vector Calculus 총정리

위의 글 내용에서 수학적인 개념을 덧붙여서 Gradient Descent를 이해해 보겠다.

Gradient Descent를 쉽게 말하면, 함수의 기울기(Gradient)를 이용해 x의 값을 어디로 옮겼을 때 함수가 최소값을 찾는지 알아보는 방법이라고 말할 수 있겠다. ->  기울기의 절대값이 크면 경사가 가파르다는 것이고, 그만큼 x의 위치가 최소값/최댓값에 해당되는 위치로부터 멀리 떨어져있는 것을 의미하게 된다. (최소값, 최대값의 기울기는 0이므로)
여기서의 사용하는 함수가 위에서 말한 예측한 값과 실제값과의 오차를 나타내는 Cost Function, J(θ)인 것이다.

J(θ)로 자주 쓰이는 오차를 나타내는 방식이 Mean Squared Error(MSE)이다.
모든 입력 데이터에 대해 (예측값에서 실제 타깃값을 뺀) 오차를 제곱하고, 2로 나눠주는 식이 일반적이다.
(2를 나누는 것은 제곱을 미분했을 때 앞으로 튀어나오는 2를 상쇄해주기 위해 사용한다고 생각하면 된다.)

결국 돌고 돌아, 우리는 예측값과 실제값 사이의 오차가 가장 작은 부분을 찾고 싶었던 것이고, 그 부분을 찾기 위해 현재 위치에서 가중치 값을 계속 업데이트해 준다면, 그 부분을 찾을 수 있겠다는 아이디어까지 이어지게 되는 거다.
그래서 파라미터를 업데이트해주기 위해 도출된 식이 아래와 같다.
θ(업데이트 가중치) = θ(현재 가중치) - α(학습률, learning rate) x ∇J(θ)(Cost Function의 기울기)

예전 글에서도 언급했지만, Gradient Descent 방법도 종류가 여러 개다.

✔️ Batch Gradient Descent (배치 경사하강법)
training set에 속한 모든 데이터들의 gradient를 계산하고(첫 번째 데이터의 오차를 구해서 Cost Function을 만들어서, 미분.. 다음 두 번째 데이터.... 딱봐도 오래 걸릴 것 같은 느낌), 그 평균을 구해서 가중치를 업데이트해주는 방식.

✔️ Stochastic Gradient Descent (SGD, 확률적 경사하강법, On-line learning modes)
training set 순서를 섞은 후, 하나의 데이터를 임의로(stochastic) 선택해서 graidient를 구하고, 가중치를 업데이트해주는 방식
분명 데이터별로 특징이 차이가 날 수밖에 없기에, 오차율과 진폭이 다른 하강법에 비해 크다.

✔️ Minibatch Gradient Descent (미니배치 경사하강법, 가장 많이 쓰이는 방식)
위의 두 방식이 각각의 장단점이 있었기에 batch와 on-line 방식의 중간 타협점을 찾은 것이 Minibatch 방식이다.
training set을 여러 개의 minibatch로 나누고, minibatch에 속한 모든 training set의 Gradient를 평균한 후 가중치는 한꺼번에 갱신 해주는 방식이다.

 

3️⃣ Linear Regression으로 머신러닝을 시작해보자!

---

자, 그럼 어디 한번 본격적으로 기계학습을 진행해보자.
위에서 정리했던 Machine Learning의 진행순서를 기반으로, 예시와 구체적인 내용까지 덧붙여서 설명하겠다.

1. feature vector와 target vector를 담은 training set이 주어지게 된다.
    - n개의 feature를 담고 있는 feature vector x가 [x1, x2 ..., xn]와 같은 형태로 주어졌다.
    - 이때 training set D가 m개의 sample일 경우 아래와 같이 정의할 수 있겠다.  
    - D={(x(1), y(1)), (x(2), y(2)), ..., (x(m), y(m)) (x는 n개의 feature를 담고 있는 feature vector, m은 sample의 개수)

2. 파라미터값을 기반으로 예측을 수행한다. (forward)
    - 파라미터 값은 θ vector로 표현했을 때, 도출되는 예측 함수 h(x)는 θ0 + θ1x1 + … + θnxn이다.
    - θ0는 통상 1로 초기화한다. (위에서 설명했을 때, b에 해당하는 부분)
    - 예측 함수 h(x)에 임의의 입력 feature vector를 대입하면 나오게 되는 y^값이 예측 수행의 결과라고 볼 수 있다.

3. 예측한 값과 실제(target, labeled) 값과의 오차 (backward)를 바탕으로 파라미터값을 update한다. (train)
    - Cost Function, J(θ)는 SGD 기준으로 오차(예측값 y^에서 타깃값 y를 뺀 값)의 제곱을 2로 나눠준 것이라 볼 수 있다.
    - Gradient는 위의 J(θ)를 θ에 대해 편미분 해준값과 같으니, 분모 2는 상쇄되어서 x값만 오차에 곱해주면 되는 꼴로 도출된다.
    - 오차는 예측값 y^에서 타깃값 y를 뺀 값이고, 예측값 y^은 θ와 x의 내적값이다. 이때, θ에 대한 편미분을 수행해주면, y는 상수취급으로 날라가게 되고, θx의 미분값 x만 남게 되는 것이다.
    - 위에서 θ(업데이트 가중치) = θ(현재 가중치) - α(학습률, learning rate) x ∇J(θ)(Cost Function의 기울기)라고 했다. 즉, ∇J(θ)에 들어가는 부분이 위에서 계산한 J(θ)를 θ에 대해 편미분 해준값 x값과 오차의 곱이라고 이해하면 되겠다.

✔️ 모델의 성능을 향상시키기 위한 방법

1. Feature Normalization
: 주어지는 특징 데이터들은 각자 다른 단위와 범위를 가지고 있기 때문에 해줘야 하는 작업이다.
예를 들어, 집의 크기(size)와 침실의 개수 feature 각각의 단위는 feet와 size로 다르고, 데이터의 대략적인 범위 역시 크기 0-2000(feet), 개수 0-5개 정도로 차이가 나게 된다.
이러한 feature data의 단위와 범위 차이는 거리 기반의 모델링(distance based model)을 수행할 때 문제가 되는데,
상대적으로 범위가 넓은 집의 크기가 거리 계산을 하는 과정에서 더 많은 기여를 하게 되어 더 중요한 변수 or 영향력이 높은 변수로 인식될 수 있다. 따라서, 이러한 문제를 방지하기 위해 데이터의 범위를 재정의하는 스케일링(scaling)을 수행해야 한다.

2. Learning Rate (α)
: 가중치 값을 업데이트할 때 우리는 Learnig Rate라는 학습률 값을 곱해주는 방식(기울기, 경사의 다음 지점을 결정하는 보폭(step)과 같은 느낌)을 사용하기 때문에 적절한 Learning Rate 수치를 지정해주는 것은 매우 중요하다.
한마디로 말해 Learning Rate값이 너무 커서도, 너무 작아서도 안된다는 말이다.
lr값이 너무 크면, 다음 step이 너무 커서 가장 낮은 지점을 찾지 못하거나, 발산할 수도 있다.
반대로 lr값이 너무 작으면, 다음 step이 너무 작아 가장 낮은 지점까지 경사를 타고 내려가는 시간이 매우 오래 걸릴 것이다.
-> 대게 1*10^-6부터 1.0까지 각각 넣어보고 가장 성능이 좋은 것을 설정해주는 방법을 사용하거나, learning rate scheduler라는 학습률을 갈수록 줄여가는 방법을 사용해서 최적의 학습률을 찾는다.

 

4️⃣ Logistic Regression: Linear Regression에 Activation Function과 MSE를 더해주자!

---

로지스틱 회귀는 주어지는 범주형 데이터(고양이, 개)에 대해 분류(0, 1)를 수행해주는 모델이다.
*더 정확하게 말하면, 0과 1 사이의 값으로 사건의 발생 가능성을 예측하는 모델이다. (아무튼 분류 모델에 속한다.)

앞에서 배운 Linear Regression 과정의 전부가 Logistic Regression 과정에 포함되며,
마지막에 Linear Regression 과정을 통해 도출되는 예측값을 Activation Function에 넣어준다는 점에서만 차이가 존재한다.

✔️ Activation Function, τ()이란?

예측값을 어느 일정한 값으로 변환을 해주는 함수라고 생각하면 된다.
Logistic Regression은 강아지, 고양이와 같은 분류를 수행해주는 모델이므로, 집 값을 예측하는 앞선 모델의 값의 형태가 아니라 0 아니면 1과 같은 클래스 숫자로 변환해줘야 한다.
그래서 사용하는 것이 Activation Function이다.
Logistic Regression에서는 Logistic Sigmoid 함수를 Activation Function으로 사용해 0과 1 사이의 확률값으로 변환을 시켜준다.

✔️ Mean Squared Error(MSE) -> Cross-Entropy(CE) Loss

Linear Regression에서 예측값과 실제값의 차이를 나타내는 loss로 MSE(Mean Squared Error) 방식을 사용했지만,
Logistic Regression에서는 MSE 대신 Cross Entropy Loss를 사용해서 Cost Function, J(θ)를 구해줄거다.

Cross Entropy Loss를 사용하는 이유는 Logistic Regression에서 사용하는 Activation Function, Logistic Sigmoid 함수의 영향 때문이다.
MSE를 사용했을 때, Cost Function J(θ)의 모양이 Linear Regression처럼 하나의 명확한 minimum 지점(극소점)을 갖는 것이 아니라 여러 개의 극소점을 갖는 wavy한 모양으로 나오기 때문에 Local Minima 문제에 빠질 수 있다는 이유다.
*Local Minima란 진짜 오차가 가장 작은 부분이 아니라, 지역적인 극소점을 가지고 Loss가 가장 작은 부분이라고 오해하는 문제라고 이해하면 되겠다.

Cross Entropy Loss를 어떻게 구하는지 알아보자.
각각의 sample에 대해서 실제 label값 y와 예측값 y^에 로그 씌운 값을 곱해주고 이를 모두 더해, sample 수로 나눠준 값에 마이너스를 취한 형태가 Cross Entropy Loss의 식이다.
말이 어려운데, 쉽게 말하면 실제 값과 로그 예측값을 곱해서 평균 내주고, 마이너스만 앞에 붙여주는 셈이다.

Loss의 핵심은 실제값과 예측값이 얼만큼 차이 나느냐에 따라서, 차이가 크면 그만큼의 큰 Loss를 반환해줘야 한다는 것이다.

즉, 어차피 1과 0중 하나일 실제값 y를 곱해주는 것은 뒤의 예측값을 상쇄시킬지 말지를 정해주기 위함에 불과하고, 결국 우리의 Loss는 예측값 확률(0~1 사이의 값)이 될 것이다.
이때, 실제값이 1일 때는 반환 확률 자체가 Loss가 되는 셈이고, 실제값이 0일 때는 1에서 반환 확률을 뺀 값이 Loss가 되도록 계산을 해줄 것이다. 그리고 이 값에 로그를 취해 0에 가까울수록 높은 Loss값을, 1에 가까울수록 낮은 Loss값을 최종적으로 반환해 준다.

✔️ Gradient of Cross-Entropy(CE) Loss

Cost Function을 구했으니, 가중치값을 업데이트해주기 위한 Gradient도 구해줘야겠다.
실제 값과 로그 예측값을 곱해서 평균 내주고, 마이너스만 앞에 붙여주던 Cross Entropy Loss를 θ에 대해 편미분 해주자.

공식 유도 과정은 아래 이미지에서 확인하면 되겠고,
결론적으로 Cross-Entropy(CE)의 Gradient는 오차(예측값과 실제값의 차이)를 입력 데이터 x와 곱해준 값이 도출된다.
여기서 놀라운 점.
Logistic Regression과 Linear Regression의 Gradient를 구하는 방식에서 최종 예측값의 activation function의 유무차이만 있을 뿐 오차와 입력 데이터 x를 곱해준다는 틀은 동일하다는 것!

 

5️⃣ Perceptron: Logistic Regression의 Activation function을 계단함수로 바꿔주자!

---

위에서 배운 Logistic Regression 과정과 동일한데,
마지막 Activation Function을 0과 1 사이의 확률값을 반환하던 Logistic Sigmoid 대신 "계단함수"를 사용하면 퍼셉트론이 된다.
계단함수는 0 이상의 값에 대해서는 1을, 0 미만의 값에 대해서는 -1을 반환시켜주는 아주 간단한 함수를 말한다.

Logistic Regression 과정과 동일하다고 해도 복습 차원에서 Perceptron의 흐름을 한번 훑어보자.

입력 데이터 xi와 가중치 wi의 곱을 feature vector의 개수만큼 모두 더해주고, 이를 계단함수에 넣어 1 혹은 -1로 반환한다.
출력값에 대한 Cost Function을 구해주고, 이를 통해 Gradient를 구해 모든 가중치를 만족할만한 성능이 나올 때까지 update 해주면 되겠다.

✔️ Perceptron의 Cost Function과 Gradient는 어떻게 구할까?

퍼셉트론의 Cost Function은 오분류된 샘플(예측값과 라벨값이 다른 경우)에 한해서만 Loss를 구해줄거다.
Loss는 Activation Function을 통과하기 전의 출력값(wTx)과 라벨값(y)을 곱해서 마이너스를 취한 값들의 전체 합으로 표현한다. (다시 한번 말하지만, 오분류된 샘플에 한해서만 구해주는 거다.)

마이너스를 붙여주는 이유는 퍼셉트론의 Cost Function이 오분류된 집합에 한해서만 Loss를 구하기 때문이다.
다시 말해, 출력값과 라벨값을 곱하면 오분류된 결과이기에 두 값의 곱은 무조건 음수가 나올 수밖에 없고 (출력값과 라벨값의 부호가 다르니까) Loss는 양수값을 가져야 가중치를 업데이트해줄 수 있으니까 마이너스를 붙여주는 것이다. 

Cost Function을 구했으니, 이 값을 미분해서 가중치를 Update 해주기 위한 Gradient를 구해주자.
wi에 대해 편미분을 취해주면, 결국은 다 날아가고 라벨값과 i번째 요소에 대한 x값의 곱에 마이너스를 취한 값들의 합만 남게 되는 것을 확인할 수 있다.
즉, 퍼셉트론의 가중치를 업데이트할 때는
기존 공식 θ(업데이트 가중치) = θ(현재 가중치) - α(학습률, learning rate) x ∇J(θ)(Cost Function의 기울기)에서 마이너스 두 개가 상충되어,
θ(업데이트 가중치) = θ(현재 가중치) + α(학습률, learning rate) x (라벨값과 i번째 요소에 대한 x값의 곱들의 합)으로 표현된다.

자세한 공식과 흐름은 아래 손풀이를 보고 참고하길 바란다.

✔️ Gradient Descent 방법에 따른 Perceptron 프로세스의 차이를 알아보자

✔️ Batch Gradient Descent (배치 경사하강법)
training set에 속한 모든 데이터들 중 오분류된 데이터 set에 대한 Gradient 평균을 계산하고, 가중치를 업데이트해준다.
-> 전체 오분류 data set에 대한 Gradient 평균값으로 파라미터를 업데이트해주는 방식

✔️ Stochastic Gradient Descent (SGD, 확률적 경사하강법, On-line learning modes)
training set 순서를 먼저 섞는다. 그리고 하나의 데이터를 임의로(stochastic) 선택한다.
해당 데이터가 오분류인 경우에 Graidient를 계산하고, 가중치를 업데이트해준다.
-> 임의의 data에 대한 Gradient값으로 파라미터를 업데이트해주는 방식

✔️ Minibatch Gradient Descent (미니배치 경사하강법, 가장 많이 쓰이는 방식)
training set을 여러 개의 mini-batch로 나눈다.
그리고 한 minibatch set에 속한 모든 데이터들 중 오분류된 데이터 set에 대한 Gradient 평균을 계산하고, 가중치를 업데이트해준다.
-> Minibatch에 속한 data들의 Gradient 평균값으로 파라미터를 업데이트해주는 방식

✔️ Perceptron과 Decision Boundary

다시 리마인드해서, 퍼셉트론은 결국 f(x) = xTw + w0​라는 선형함수에 의해 예측을 하는 모델이라고 말할 수 있었다.

이때, 위의 선형함수 f(x)에 의해 결정될 수 있는 (feature space가 n차원일 경우, n-1차원의) 초평면 d(x) = xTw + w0​ = 0를 결정경계(Decision Boundary)라고 부를 것이다.
위 초평면을 나타내는 방정식에서 w는 법선 벡터 (normal vector) 즉 초평면의 방향을 결정하는 요소라고 볼 수 있고,
bias b는 원점에서 얼마나 떨어져 있는가를 나타내는, 초평면의 위치를 결정하는 요소라고 볼 수 있겠다.

 

6️⃣ Neural Network & MLP (Multi-Layer Perceptron): Perceptron의 한계를 극복하기 위한 노력

---

Perceptron의 한계는 명확하다.
Decision Boundary로 100% 선형 분리가 불가능한 경우가 아래 그림과 같이 존재한다는 내용이다. (간단 XOR 분류 문제의 경우에도 직선 하나로는 100% 분류 예측을 수행할 수가 없기 때문이다.)
이 한계를 극복하기 위해 등장한 개념이 바로 퍼셉트론 층을 여러개 쌓으면 된다는 아이디어, MLP(Multi-Layer Perceptron)이다.

지금부터는 MLP의 핵심 아이디어들을 차근차근 살펴보면서, MLP가 어떻게 이루어지는지 알아보도록 하겠다.
아마 이 글에서 가장 중요한 부분일거다.

Perceptron의 한계: 위와 같은 데이터에 대해 하나의 선형 결정 경계로는 100% 예측을 수행할 수 없다.

✔️ 활성함수 (Activation Function)는 다시 Logistic Sigmoid 함수로

Preceptron에서는 1과 -1로만 출력하는 계단 함수를 사용했는데,
Multi-Layer Perceptron에 와서는 다시 Logistic Sigmoid (0~1 사이의 값을 출력)를 Activation Function으로 사용할 거다.
*Deep Neural Network로 넘어오면 ReLU를 Activation Function으로 사용할 거다.

Activation Function을 바꿔준 이유는 둘 중에 하나의 값으로만 반환하는 계단함수는 특징공간을 변환할 때, 영역을 점으로 밖에 변환할 수가 없기에, 영역을 영역으로 변환해 줄 수 있는 연성 활성함수(출력이 연속된 값)를 사용하는 것이다.

✔️ Hidden Layer (은닉층)의 도입

MLP에서 가장 핵심적인 부분이다.
은닉층(Hidden Layer) 아이디어가 MLP에서 등장한 이유는 여러 개의 Perceptron(= 여러개의 Decision Boundary)을 사용하기 위해서다.

Hidden Layer에서는 feature vector에 대해 가중치를 곱해 모두 더하고, activation function에 넣어주면서 최종 y를 반환했던 하나의 퍼셉트론이 병렬로 여러 개가 존재한다. 
이것을 "퍼셉트론이 병렬적으로 결합한 형태", "하나의 층"과 같은 모습을 띄기 때문에, Hidden Layer(은닉층)라고 부르는 것이다.
퍼셉트론이 여러개가 있으니 결정 경계도 여러개가 생길 것이고, 이 여러 개의 퍼셉트론들을 다시 순차적으로 결합해서 새로운 sapce로 변환해주는 작업도 가능하게 되는 것인데,
즉, Hidden Layer를 통해서 기존에 있던 feature space를 새로운 feature space로 변환을 할 수 있게 되는 아이디어로 이어지는 것이다.
=> 여러 번의 은닉층을 거치면, 분류에 더 유리한 새로운 feature space로 변환되고, 이를 통해 입력 데이터의 특징이 더 잘 추출된다. [이를 기계학습에서는 표현 학습 (representation learning)이라 부른다.]

결론적으로, 1개 (나중에는 n개로 확장되겠지)의 Hidden Layer(= 여러 개의 Layer (입력층, 은닉층, 출력층)가 존재하는 모델)가 존재하는 모델, 이것이 바로 우리가 계속 마주치게 될 MLP(Multi-Layer Perceptron) 모델이다.

Hidden Layer를 통해 기존의 feature space를 새로운 featue space로 변환한다는 개념의 이해

✔️ MLP Architecture (입력층, 은닉층, 출력층, Parameter) 정리해보기!

1️⃣ 입력층 : 입력층 노드(neuron이라 부름)의 개수 d+1개는 주어지는 데이터에 의해 정해진다.
    - 입력층 노드의 개수가 d+1인 이유는, 데이터에서 주어지는 입력 특징의 개수 d개에 bias term까지 합해서 나오는 개수이다.

2️⃣ 은닉층 : 은닉층의 개수나 각 은닉층의 노드 개수는 사용자가 직접 지정해야 하는 하이퍼 파라미터(hyper-parameter)다.
    - 아래 그림은 은닉층이 1개인 경우이고, 이를 2층 Perceptron이라 부른다. (Θ = { U1, U2 })

3️⃣ 출력층 : 출력층 노드의 개수 c개는 주어지는 데이터에 의해 정해지는 정답 벡터의 차원과 같다.
    - 정답 벡터의 차원과 출력층 노드 개수가 같은 이유는, Classification 문제의 경우 한 노드에 개/고양이 분류를 했던 예전과는 다르게 정답 벡터를 One-Hot-Encoding(정답 index만 1로 나머지는 0으로 표현하는 방법 - 예를 들어, 개는 10, 고양이는 01과 같이 표현하는 방법이다.) 방식으로 표현을 해줄 것이기 때문이다.
    - One-Hot-Encoding을 사용하는 이유는 index의 수가 커질수록(개는 1, 고양이는 2와 같이) 특정한 의미를 갖는 것이 아니기 때문이다.

4️⃣ 가중치(Parameter) 
    - 기본적으로, 위첨자는 몇 번째 층에 연결되는지를 나타내고, 아래첨자는 앞이 연결대상의 노드 번호, 뒤가 연결 시작점의 노드 번호라고 이해하면 된다. (위첨자를 제외하고 u_ji인 경우에는 i번째 노드로부터 j번째 노드와 연결되는 가중치인 것이다.)
    - 가중치 하나인 스칼라, j번째 노드에 연결된 모든 가중치인 Column Vector, 층에 연결되는 모든 가중치인 Matrix로 다양하게 표현할 수 있다. (자세한 표기법은 아래 오른쪽 그림을 참고하길 바란다.)

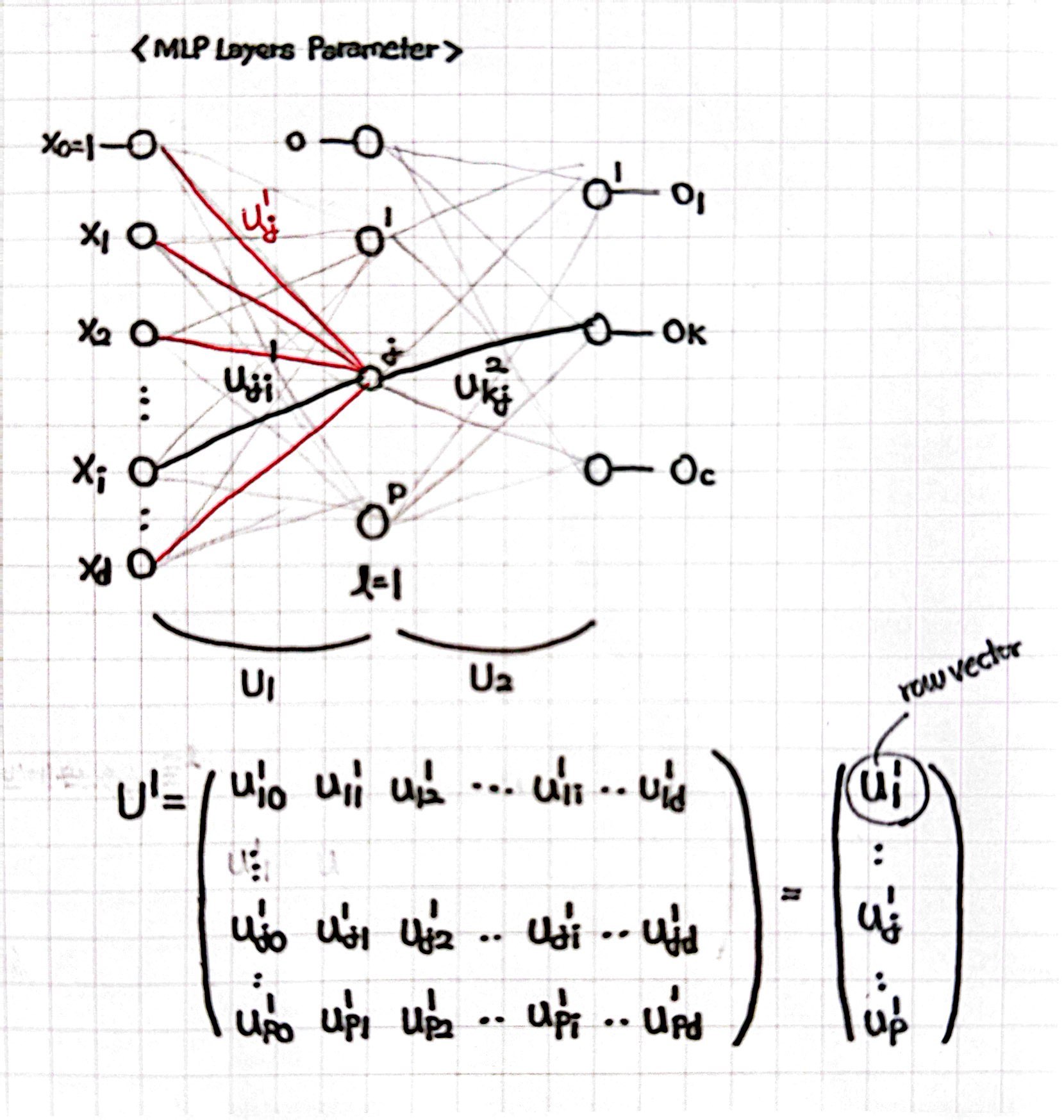
✔️ MLP의 Forward Computation

위에서 MLP의 개념, Layer의 형태, 그리고 Layer와 Parameter의 출력 표기법을 배웠으니, 전방계산(Forward Computation)을 이해해볼 차례이다.
표기가 헷갈려서 그렇지, 결론적인 내용은 지금까지 했던 내용의 반복이라고 볼 수 있다.

j번째 노드에 대한 연산은 j번째 노드와 연결된 모든 feature vector(x)와 weight(parameter) vector(wj)의 내적으로 계산할 수 있으며, 이 내적값을 Activation Function에 넣어줌으로써 마무리된다. (은닉층이나 출력층이나 이 프로세스를 따른다.)
다만 이 과정을 각각의 노드 인덱스의 표기와 가중치 인덱스의 표기, 그리고 몇 번째 Layer에서 수행하는 연산이냐에 따라 다르게 표현해줄 수 있기에 어렵게 느껴질 뿐인 것이다.

✔️ MLP의 Error Back-Propagation(오류 역전파) 알고리즘 사용

위에서 예측을 수행했으니, 가중치를 업데이트해주기 위해 Cost Function을 구하고 Gradient를 구해줄 차례이다.
Mean Squared Error(MSE)를 기준으로 오차를 구해줄 것이고, 구해진 Cost Function을 가중치에 대해 편미분해줘서 나온 값을 learning rate와 곱해서 기존 가중치값과의 차를 업데이트해주자.
*θ(업데이트 가중치) = θ(현재 가중치) - α(학습률, learning rate) x ∇J(θ)(Cost Function의 기울기)

문제는 Gradient의 기울기를 구하는 것이 복잡해졌다는 것이다.
Chaine Rule을 사용한 미분이 많아지다보니 몇 가지 과정을 거쳐야 하는데, 이는 앞에서 설명한 용어가 그대로 들어가 있으니 앞의 내용을 정확하게 숙지하고 아래 풀이 그림을 살펴보길 바란다.

아무튼, 2층 Perceptron이라 했을 때 기준으로 살펴봤을 때,
출력층 Gradient의 영향을 미치는 녀석들은 오차(출력값과 라벨값과의 차이), 출력층 활성함수의 미분값, 출력층에 들어온 입력 feature이다. (= 오차가 클수록, 활성함수의 미분값이 클수록, 입력 feature가 클수록 parameter는 더 많이 update 되는 셈!)
은닉층 Gradient의 영향을 미치는 녀석들은 해당 은닉층 노드와 관련된 모든 오차(출력값과 라벨값과의 차이), 모든 출력층 활성함수의 미분값, 모든 출력층 가중치 column vector들이고, 여기에 은닉층 활성함수의 미분값, 은닉층에 들어온 입력 feature까지이다.
-> 말이 어려워서 그렇지 즉, 내가 구하고 싶은 weight값과 연결된 모든 값들이 Gradient에 영향을 끼치는 셈이다.
이러한 복잡한 식들을 이용해서 출력층의 오류를 역방향(왼쪽)으로 가면서 Gradient를 계산하는 알고리즘을 머신러닝에서는 오류 역전파(error back-propagation) 알고리즘이라 부른다.

 

7️⃣ Muiticlass Classification: 여러개의 클래스를 분류하기 위한 Softmax Function의 사용

---

✔️ Activation Function의 변경: Logistic Sigmoid -> Softmax

위에서, 주어진 이미지를 가지고 강아지와 고양이를 분류(Classification)하는 문제는 Logistic Regression으로 풀 수 있다고 설명했었다.
입력값과 파라미터 값을 내적해서 도출한 예측값에 Logistic Sigmoid Activation Function을 적용시키면, 0과 1 사이의 확률값으로 변환을 해줄 수 있다고 배웠는데, 이번에는 강아지와 고양이뿐만 아니라 닭, 호랑이 등등... 분류해야 하는 클래스가 여러 개인 경우를 다룬다.

Logistic Sigmoid를 적용할 수는 없다.
출력층의 한 노드가 "강아지 vs 나머지 클래스"로 분류하게 만들 경우에는 클래스의 불균형 문제가 발생하게 될 것이고,
출력층의 한 노드가 "강아지 vs 고양이, 고양이 vs 호랑이"와 같이 만들 경우에는 너무 많은 이진 분류기가 필요하게 될 것이다.
그래서 등장한 것이 Softmax Activation Function이다.

Softmax는 클래스의 개수와 같은 c개의 출력 노드들의 전체 합을 1로 만드는 함수이다.
즉, 출력 노드들의 하나하나의 값이 해당 클래스일 "확률"과 같은 의미가 되는 셈이니 우리는 가장 높은 확률을 가질 노드에 대해 예측값으로 반환해 줄 수 있다는 것이다.

결론적으로, 여러 개의 클래스에 대해 분류를 수행하는 Multiclass Classification은 모든 과정을 예전에 배웠던 내용과 동일하게 진행하되, "마지막 Activation Function을 Softmax로 사용한 모델이다."라고 받아들이면 되겠다.  

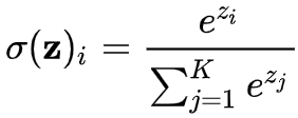
✔️ Muiticlass Classification의 Cost Function과 Gradient

Logistic Regression에서 Cost Function으로 Cross Entropy Loss를 사용했던 것과 마찬가지로,
분류 문제인 Muiticlass Classification에서도 Cross Entropy Loss를 활용해서 J(θ)를 구해줄 것이다.

원리는 위와 똑같다.
"실제 값과 로그 예측값을 곱해서 평균 내주고, 마이너스만 앞에 붙여주는 형식"이다.
단, 이진 분류의 경우에는 분류기가 하나였기에, 실제값이 1일 때와 0일 때 두 가지 경우로 나누어서 공식을 써주었다면, 다중 분류는 분류기가 클래스의 개수 K와 같기 때문에 K개의 분류기에 대해 모두 Loss를 구해줘야 한다는 점이 차이점이다.
*예측값의 Activation Function이 Logistic Sigmoid인지, Softmax인지도 역시 차이점이기는 하다.

Gradinet도 마찬가지 방식으로 구해주면, "오차(예측값과 실제값의 차이)를 입력 데이터 x와 곱해준 값"이 도출되는 것을 확인할 수 있었다.

 

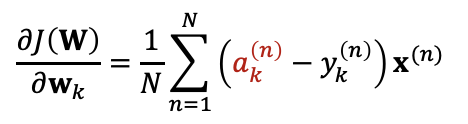
8️⃣ Model Evaluation: 모델의 성능을 확인해보자!

---

지금까지 우리는 어떤 데이터가 컴퓨터에게 주어졌을 때,
그 데이터가 강아지인지 혹은 고양이인지 예측(Classification, 분류) 하거나, 혹은 주어진 조건들로 집값이 어떻게 될지 예측(Regression, 회귀)하는 방법들에 대해 공부했었다.
과정은 전반적으로 입력값과 파라미터값을 내적해 예측값을 도출했고, 이 예측값과 실제값과의 오차를 기반으로 한 Gradient를 구해 파라미터값을 만족할만한 모델 성능이 나올 때까지 지속적으로 업데이트해주는 내용이 전부였다.

그렇다면 여기서 드는 의문.
"만족할만한 모델의 성능"을 내기 위해 개발자는 "어떻게 모델의 성능을 평가할 것인가?"라는 질문이 생긴다.

지금부터는 이 질문에 대한 해답을 얻는 내용의 글이 되겠다.

✔️ Evaluation의 핵심은 model의 generalization performance를 확인하는 것!

보통 우리는 주어지는 데이터의 feature vector와 labeled data를 모델에 학습(fit)시켜 성능을 지속적으로 향상시킨다.

하지만, 여기서 생기는 의문.
결국 우리가 모델의 성능을 향상시키는 이유는 학습한 데이터가 아니라, 모델이 처음 보는 데이터에 대해 높은 정확도로 예측하기를 바라는 것인데, feature값과 label값을 모두 알고 있는 이 데이터들이 처음 보는 데이터들을 대표한다고 말할 수 있을까?

이미 최종 올바른 답까지 알고있는 이 데이터로 성능을 측정해봤자,
측정되는 정확도는 진정한 모델의 예측 정확도를 나타낸다고 할 수 없을 것이다. (이미 모델이 답을 알고 있잖아.)
즉, 우리가 모델을 Evaluation할 때는, 이미 알고있는 데이터가 아니라 모델이 알지 못하는 데이터 (unseen data)에 대해 해줘야 한다는 뜻.
이를 model의 generalization performance를 Evaluation 해준다고 말한다.

✔️ 3-Way Holdout Method Process (Training/Validation/Test Set)

모델을 훈련시키고, 최적의 하이퍼파라미터를 찾고, 모델의 성능을 Evaluation하기 위해 데이터를 3개로 나눠줄 것이다.
1️⃣ Training Set : 모델을 훈련할 때 사용하는 데이터 세트 -> model fitting
2️⃣ Validation Set : 모델을 선택하거나, 최적의 하이퍼파라미터를 정할 때 사용(모델의 generaliztion 성능을 여기서 확인하는 느낌)하는 데이터 세트 (훈련을 시키는 것과 다름!) -> model selection
3️⃣ Test Set : 최종 모델에 대한 성능을 Evaluation할 때 사용하는 데이터 세트 (절대 라벨 데이터를 모델이 알아서는 안된다!) -> model test

이렇게 데이터를 나누면 아래와 같은 순서대로 Machine Learning에서 데이터를 사용하게 된다.
1️⃣ 같은 Training Set을 가지고, hyperparameter를 다르게 변경하면서 모델을 Train 시킨다.
2️⃣ Validation Set으로 모델의 generalization performance를 비교하고, 최적의 hyper parameter를 선택한다. -> Train Score와 Validation Set으로 나온 Test Score를 비교하면서 차이가 가장 작은 지점에서 Early Stopping을 사용한다.
3️⃣ Test Set으로 모델의 최종 generalization 성능을 확인한다.
➕ (선택사항) 모든 데이터(Train+Valid+Test)에 대해 딱 한번 retrain 시킨다. (많은 데이터를 한번 이용해보는 셈)

✔️ Cross-Validation (Leave-one-out Cross-Validation, k-Fold Cross-Validation)

이렇게 데이터를 Train, Validation, Test Set로 나눠주면 되는데, 이렇게 사용할 수 없는 경우도 있다.
바로 데이터의 양이 너무 적은 경우.
애초에 학습시키기에도 데이터가 너무 부족한데, Train/Validation/Test으로 나누면 학습시킬 데이터가 더더욱 부족해지게 되는 것.
이런 경우를 모델의 배움이 부족한 경우, Underfitting이라고 부른다.

이런 경우 사용할 수 있는 방식이 Validation으로 사용할 데이터를 서로 돌아가면서 지정하는 Cross Validation 방식이다.
Cross Validation은 크게 두 종류가 나뉜다.
데이터 하나만을 뽑아 반복해서 Validation하는 Leave-one-out Cross-Validation 방식과, k개의 데이터 set을 나누어 한번씩 돌아가며 Validation Set으로 활용하는 k-Fold Cross-Validation 방식이 있고,
이 두 가지 경우에 대해 모두 공통적으로 별도의 Test Set은 만들어줄 수 없다는 점까지 같이 기억해두자!