2023. 10. 2. 22:05ㆍDeveloper Basis
⚠ 이 글은 머신러닝 공부용으로 보기 위해 작성한 Probability and Random Variables(확률이론) 정리글입니다. ⚠
머신러닝에 필요한 확률과 랜덤변수의 개념 위주로 정리되어 있어, 확률론의 전반적인 지식을 배우고 싶다면 이 시리즈의 내용으로는 부족할 가능성이 매우 높습니다. 권장하지 않습니다.
또한 제가 알아볼 수 있도록 쉽게 정리한 글이니, 오개념이나 수학적으로 잘못된 내용이 있을 수도 있습니다. 저를 너무 믿지 마세요.
댓글로 지적해 주시면 빠르게 수정하겠습니다:)
1️⃣ 확률을 본격적으로 배우기 전, 용어정리부터 하고 넘어가자
- Probability(확률)이란?
: 불확실성(uncertainty)과 무작위성(randomness)을 정량화하기 위한 논리적인 뼈대(logical framework) - Random Experiment란?
: 동일한 조건(same conditions) 하에 실험을 반복할 때, 결과를 알 수 없고(unknown) 예측할 수 없는(unpredictable) 실험
(예시: 주사위 던져서 눈 확인하는 실험, 동전을 던져서 앞과 뒤를 확인하는 실험) - Outcome이란?
: Random Experiment에 대해 가능한 모든 관찰 (any possible observation) - Sample Space란?
: 일어날 가능성이 있는 모든 outcome들의 집합, 각 outcome들은 상호 배타적(mutually exclusive)이고 집단적으로 완전(collectively exhaustive)하다. 주사위 실험에서의 Sample Sapce S는 {1, 2, 3, 4, 5, 6}이다. - Mutually Exclusive하다는 것은?
: 사건들의 집합 A1, A2, A3 .... An이 있다고 할 때, 임의의 사건 두 개 Ai, Aj (i와 j는 같지 않다)의 교집합이 없다는 것을 의미한다. - Collectively exhaustive하다는 것은?
: 사건들의 집합 A1, A2, A3 .... An이 있다고 할 때, A1부터 An까지 사건들의 합집합이 전체가 된다는 것을 의미한다. - Events란?
: 실험 결과들의 집합(set of outcomes of an experiment)이다. = sample space의 부분집합(subset)으로 정의할 수 있다.
2️⃣ 기초 Probability Theorems
[Axioms of Probability]
지금부터 배우게 될 모든 확률 이론은 이 3개의 Axioms를 기반으로 확장되는 개념들입니다.
👍🏻 임의의 events A에 대해 P[A] >= 0을 만족한다. -> non-negativity Axioms
✌🏻 P[S] = 1을 만족한다. (S는 Sample Space를 의미) -> normalization Axioms
🤟🏻 상호배타적(mutually exclusive)인 셀 수 있는 events의 집합에 대해 P[A1 U A2 U ...] = P[A1] + P[A2] + ... 를 만족한다.
지금부터 알아두어야할 기본 확률의 이론들에 대해 하나씩 알아가보겠다.
말로 표현하면 어렵게 느껴질 수 있지만, 사실 식으로 표현하면 아무것도 아닌 내용이다. 하지만, 중요한 내용이니 꼭 읽어보자. 그리고 아래 그림으로 이 말을 이런 식으로 표현하게 되는거구나하고 이해해보자.
첫째. 상호배타적(mutually exclusive)인 두 사건에 대해 두 사건 합집합의 확률은 각 사건의 확률을 더한 것과 같다. (두 사건이 아니라 사건 개수의 범위를 늘려도 성립)
-> 확장) 사건 B = {S1, S2, ..., Sm}의 확률 P[B]는 사건에 포함된 각 결과의 확률 P[{Si}]의 합과 같다.
둘째. 어떤 두 사건 합집합의 확률은 각 사건의 확률을 더한 것에서 교집합의 확률을 뺀 것과 같다. (mutually exclusive 조건이 들어가지 않았을 때, mutually exclusive한 경우에도 적용이 가능하다. 교집합의 확률은 0이므로.)
셋째. 공집합의 확률은 0이다.
넷째. A 여집합의 확률은 1에서 사건 A의 확률을 뺀 것과 같다.
다섯째. Sample Space S = {S1, ..., Sn}의 각각의 결과 Si가 equally likely 하다면, P[{Si}]는 전체 outcome의 개수를 1로 나눈 값과 같다.

3️⃣ 조건부 확률(Conditional Probability)과 파티션(Partition)
조건부 확률(Conditional Probability)이란 어떤 사건(B)이 일어났다는 전제하에 다른 사건(A)이 일어날 확률을 말한다.
*어떤 사건 B를 부분 정보(partial information)라고도 부른다.
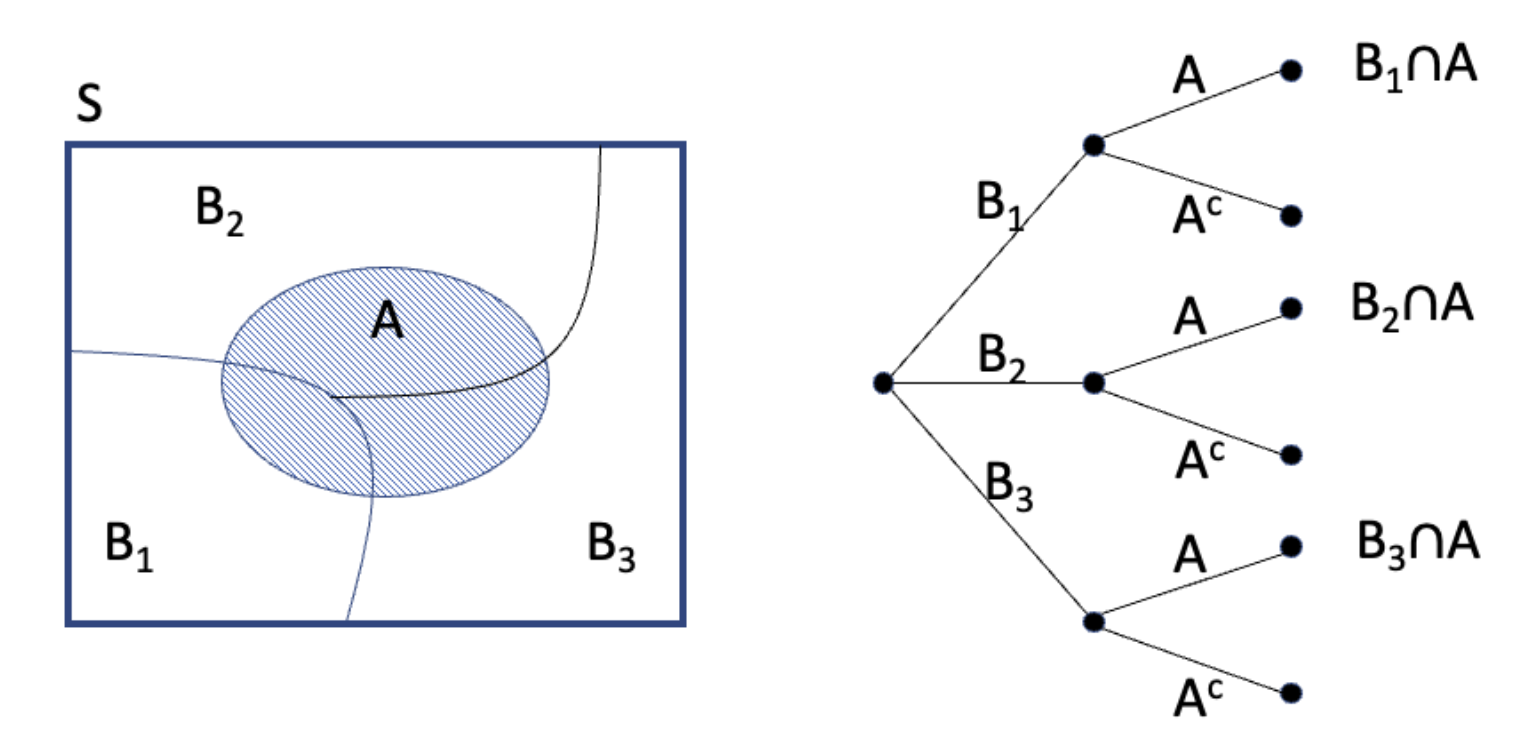
확률 공리(Axioms of Probability)를 따라 적용될 수 있는 조건부 확률의 특성 3가지가 존재한다. (아래 오른쪽 그림 참조)
조건부 확률의 예시 문제는 아래와 같다.
- 주사위를 연속적으로 두 번 던지는 실험에서 주사위 눈의 합이 9라고 할 때, 첫 번째 주사위 눈이 6일 확률은?
- 동전을 연속해서 3번 던지는 실험이 있을 때 P[A | B]를 구하라. A = {head가 tail보다 더 많이 나온 사건}, B = {첫 번째 동전이 head인 사건}



파티션(partition)은 Collectively exhaustive하고, mutually exclusive한 events의 집합이다.
*Collectively exhaustive와 mutually exclusive의 개념은 1️⃣번 파트에 정리되어 있으니 모르겠다면, 다시 올라가서 확인해 보자.
아래 B1, B2, B3, B4로 나누어져 있는 Sample Space의 모습이 partition이다.



이 파티션의 개념에서 나올 수 있는 이론을 같이 배워보겠다. (위의 그림 참조)
파티션 B = {B1, B2, B3, B4}와 어느 특정한 사건 A, 그리고 A와 Bi의 교집합을 Ci라고 표현한다고 할 때, 너무도 당연하게 A는 C1부터 C4까지의 합으로 표현할 수 있고, 이는 다시 A와 Bi와의 교집합 간의 전체 합으로도 표현가능하다. -> 직관적으로 그림으로 이해할 수 있을 거라 생각한다.
이 개념을 바탕으로 P[A]의 확률은 P[A]와 파티션 Bi간의 교집합의 전체 합으로 나타낼 수 있다는 이론이 도출된다.
4️⃣ 전체 확률의 법칙(Law of Total Probability)과 베이즈 정리(Bayes' Theorem)
위에서 배운 조건부 확률과 파티션을 기반으로 도출되는 확률에서의 두 가지 중요한 공식을 배워보자.
전체 확률의 법칙 (Laws of Total Probability)과 베이즈 정리 (Bayes' Theorem)이다.
[전체 확률의 법칙 (Laws of Total Probability]
쉽게 말해서 사건 A의 확률을 A와 파티션 B와의 교집합 간의 합으로 나타내는 방식이다.
위 파티션에서 배웠던 이론 내용과 일맥상통하는 내용이다. (P[A]의 확률은 P[A]와 파티션 Bi간의 교집합의 전체 합으로 나타낼 수 있다)
*결국 전체 확률의 법칙에서 문제를 쉽게 풀기 위한 가장 핵심은 "파티션을 어떻게 설정하는가"라고 봐도 된다.

[베이즈 정리 (Bayes' Theorem)]
너무도 중요한 개념이다.
베이즈 정리(Bayes' Theorem)는 조건부 확률을 구하는 공식이다.
A와 B의 교집합의 확률을 P[A | B]P[B]로 표현했다고 생각하면 되고, 만약 B가 파티션일 경우에 위에서 배운 전체 확률 법칙을 함께 적용할 수 있다는 특징을 가졌다. (이렇게 봤을 때 그저 수식으로 말장난을 친 것 같다.)


5️⃣ 독립(Independence)의 개념, 상호배타적(mutually exclusive) 개념과의 차이
사건 A와 B가 독립(Independence)할 경우, P(A, B) = P[A]P[B]가 성립한다.
즉, 이를 조건부 확률(Conditional Probability)로 확장할 경우에 P[A | B] = P[A], P[B | A] = P[B]를 만족시키게 되는데,
수식상으로도 이해할 수 있지만, 독립의 개념으로 생각해 보면 더 이해가 쉽다.
두 사건이 독립(Independence)하다는 것은 "두 사건이 서로 영향을 미치지 않는 관계"라는 것을 의미한다.
즉, 어떤 사건이 발생했을 때 다른 사건이 일어날 확률을 구하는 조건부 확률에서는 "어떤 사건이 발생했거나 말거나 상관없이 그저 뒤의 다른 사건이 일어날 확률"이 조건부 확률값이 되는 것이다. (P[A | B] = P[A], P[B | A] = P[B]의 의미)
여기서 매우 중요.
두 사건 A, B가 Independence 하다는 것과 mutually exclusive 하다는 것은 다르다.
독립의 개념은 두 사건이 서로 영향을 미치지 않는 관계 (네 갈 길 가시고, 내 갈 길 가겠소 같은 느낌)라면,
상호배타적의 개념은 두 사건이 반드시 겹쳐서는 안 되는 관계 (두 사건이 서로 엄청나게 의식하면서 영향을 끼치는 느낌)이기에 엄연히 두 개념은 구분된다고 볼 수 있다.
6️⃣ Counting Methods
지금부터 배워볼 개념은 위에서 배운 내용과 살짝 느낌이 달라진다.
확률 이론에서는 기본적으로 한 실험에서의 sample space를 파악하는 것이 중요하다. 이전까지는 그 sample space가 문제에서 이미 제시되어있는 느낌이었다면, 지금부터는 순차적인 실험에서 sample space의 outcome 개수를 결정하는 방법에 대해 배워볼 것이다.
[Fundermental Principle of Counting]
여러 개의 하위 실험(subexperiment)으로 구성되어 있는 하나의 실험이 있다고 하자.
이때, 가능한 outcome의 개수는 각각의 하위 실험들의 outcome 개수의 곱으로 나타낼 수 있다.
예시) 동전을 던지는 실험과 주사위를 던지는 실험의 outcome은 동전을 던지는 실험의 outcome 2와 주사위를 던지는 실험의 outcome 6의 곱인 12이다.
[Permutation]
서로 다른 n개의 object를 k개만큼 뽑아서 배열(순서대로 배치)하는 경우의 수
예시) 1부터 10까지 있는 카드 더미에서 3개를 뽑아 나열하는 경우를 구해야 할 때, 첫 번째 나올 수 있는 경우는 10, 두 번째 나올 수 있는 경우는 9(이미 한 장 뽑았으니까), 세 번째 나올 수 있는 경우는 8(이미 두 장 뽑았으니까). 즉 10 x 9 x 8의 결과가 나온다.

[Combination]
서로 다른 n개의 object 중에서 k개의 object를 선택하는 경우의 수
(n, k)와 (n, n-k)는 같은 답을 도출하니 상황에 맞게 (숫자가 너무 커질 경우) 적절하게 사용하자.
예시) 전체 카드 더미 중 5개의 카드를 뽑는 실험, 120명 중에서 60명의 학생을 선발하는 경우, 11명의 팀 중에서 5명의 선발 라인업을 추려야 하는 경우


[Sampling with Replacement]
서로 다른 m개의 object를 중복을 허락해 n번 뽑을 수 있는 경우는 m^n으로 표현할 수 있다.
예시) 길이가 10인 binary sequence는 2^10=1024의 outcome이 존재, 4글자 알파벳 단어의 경우는 26^4=456976의 outcome이 존재
[Multinomial Coefficient]
Multinominal Coefficient의 개념은 아래 내용에서 시작한다.
Sample Space S = {0, 1}이고, 0이 n0회, 1이 n1 = n-n0회 나타나는 경우의 observation sequence의 number는 (n, n1)이라고 표현할 수 있다. 이 내용을 일반화해 보자.
S = {So, ..., Sm-1}의 Sample Space가 있는 subexperiment를 n번 반복해서 수행한다고 할 때, n = n0+ ... + nm-1이라고 표현할 수 있을 것이다.
이때 임의의 outcome인 si가 ni번 출현할 경우의 수는 아래 왼쪽과 같이 표현할 수 있다는 의미다.

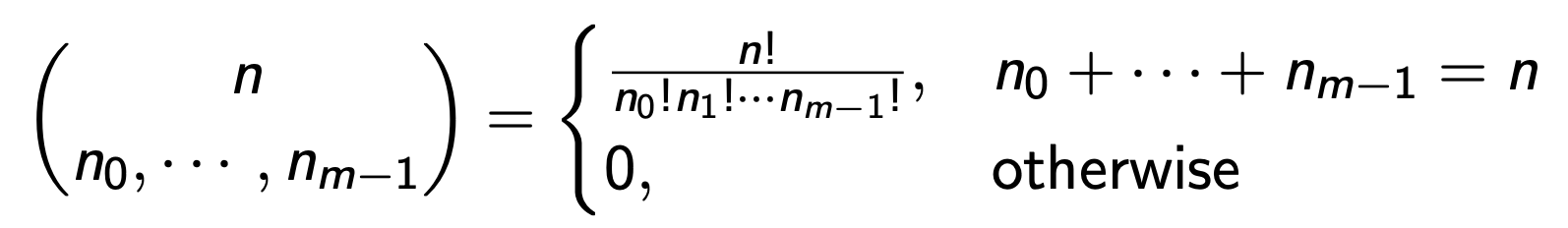
말만 들어서는 조금 어려운데, 예시를 들으면 쉽게 이해할 수 있다.
주사위 10번 던지는 실험이 있을 때, Sample Space S는 {주사위의 눈} = {1, 2, 3, 4, 5, 6}이 될 것이다.
그리고 1의 눈이 1번, 2의 눈이 1번, 3의 눈이 4번, 4의 눈이 2번, 5의 눈이 0번, 6의 눈이 2번 나오도록 한다면, 이 공식에 따라 나올 수 있는 경우의 수는 10! / 1! 1! 4! 2! 0! 2!이 되는 셈이다.
7️⃣ Independent Trials
위에서 독립(Independence)의 개념이 두 사건(events) A, B가 서로 영향을 미치지 않는 관계라고 배운 적이 있었다.
이를 조금 변형해서 연속적으로 수행하는 실험(sequential experiment)이 있을 때, 그 하위 실험 각각이 독립적으로 수행되는, 즉 서로 영향을 끼치지 않는 실험이 이번에 배울 "독립시행(Independent Trials)"의 개념이다.
예시로 이해해보자.
먼저 성공과 실패 두 가지의 경우만 존재하는 예시이다.
높이 뛰기를 5번 도전하는 실험에서 성공 확률이 p라고 할 때, 3번의 성공과 2번의 실패가 있을 확률을 구하라는 문제가 있을 수 있다.
이때 도출되는 공식은 "서로 다른 5개 중 3개의 object를 뽑는 경우 x 성공 확률(p)^3 x 실패 확률(1-p)^2"라고 도출된다.


이를 두 가지가 경우가 아닌 여러 경우가 존재하는 경우에는,
위에서 배운 Multinomial Coefficient의 경우의 수와 각 경우의 확률을 곱해주는 식으로 확장된다고 생각하면 되겠다.
2탄으로 이어집니다...⭐️
[Probability and Random Variables] 머신러닝을 위한 확률이론 총정리 (2): Random Variable Part
⚠ 이 글은 머신러닝 공부용으로 보기 위해 작성한 Probability and Random Variables(확률이론) 정리글입니다. ⚠ 머신러닝에 필요한 확률과 랜덤변수의 개념 위주로 정리되어 있어, 확률론의 전반적인
mini-min-dev.tistory.com
'Developer Basis' 카테고리의 다른 글
| [ML] 내가 머신러닝 진짜 알기 쉽게 정리해서 올려줄게 (23.10.19.ver) (1) | 2023.10.13 |
|---|---|
| [Calculus] Gradient Descent를 이해하기 위한 Vector Calculus 총정리 (1) | 2023.10.06 |
| [Linear Algebra] 머신러닝을 위한 선형대수 총정리 (上 ) (0) | 2023.10.01 |
| [Basis] 내가 보려고 정리하는 개발 용어 사전 (1) - 프레임워크(Framework)와 라이브러리(Library) (0) | 2023.05.29 |
| [GitHub] 깃허브에서 Create a new release를 눌러보자 (0) | 2022.01.08 |
