2023. 10. 18. 21:17ㆍDeveloper Basis
⚠ 이 글은 머신러닝 공부용으로 보기 위해 작성한 Probability and Random Variables(확률이론) 정리글입니다. ⚠
머신러닝에 필요한 확률과 랜덤변수의 개념 위주로 정리되어 있어, 확률론의 전반적인 지식을 배우고 싶다면 이 시리즈의 내용으로는 부족할 가능성이 매우 높습니다. 권장하지 않습니다.
또한 제가 알아볼 수 있도록 쉽게 정리한 글이니, 오개념이나 수학적으로 잘못된 내용이 있을 수도 있습니다. 저를 너무 믿지 마세요.
댓글로 지적해 주시면 빠르게 수정하겠습니다:)
앞선 [Probability and Random Variables Series] 1탄:Probability, Experiment Part 글에서 이어지는 내용입니다.
[Probability and Random Variables] 머신러닝을 위한 확률이론 총정리 (1): Probability, Experiment Part
⚠ 이 글은 머신러닝 공부용으로 보기 위해 작성한 Probability and Random Variables(확률이론) 정리글입니다. ⚠ 머신러닝에 필요한 확률과 랜덤변수의 개념 위주로 정리되어 있어, 확률론의 전반적인
mini-min-dev.tistory.com
8️⃣ Random Variable
앞에 부분까지는 <Probability and Random Variables>라는 과목 안에서 "Probabilty (확률)" 쪽을 중점으로 살펴봤다면, 지금부터는 "Random Variables (랜덤 변수, 확률 변수)" 쪽을 살펴보겠다.
누군가 나에게 Random Variable이 무엇이냐라고 묻는다면, 나는 "Random Variable은 함수다"라고 말해줄 수 있겠다.
함수는 함수인데 어떤 함수이냐면, Sample Space 내에 있는 각각의 outcome들에 대해 임의의 실수값으로 대응시키는 함수이다.
표기는 알파벳 소문자 볼드체 (x, y, z ...)로 한다.
이름은 변수인데, 개념은 함수이고, 임의의 실수값은 무엇인지... 조금 와닿지 않아 그림과 설명을 통해 더 자세하게 이해해보자.
아래 그림에 Sample Space, S 안에 있는 outcome s1, s2가 있다.
이 outcome들을 random variable x에 각각 넣어 실수축 위에 위치한 값 x와 y로 대응 (x, y가 아니라 x1, x2..이런 식으로 대응 관계를 표현하는 게 일반적이다) 시켜준다.
이때 Sample Space, S에 속해있는 x(s) = x를 만족하는 각각의 sample point (s1, s2....)들의 집합(set)을 강조하기 위해 {x(s) = x}라고 표현한다.


Random Variable에도 여러 종류가 있다.
- 어떤 임의의 random variable x의 범위가 Sx = {x1, x2, x3, ..}과 같이 countable set (셀 수 있는 집합)일 때는 Discrete Random Variable이라 부른다. -> 이번 글에서 다루는 내용!
- 어떤 임의의 random variable x의 범위가 Sx = {x1, x2, .., xn}과 같이 finite set (유한 집합)일 때는 Finite Random Variable이라 부른다.
- 어떤 임의의 random variable x의 범위가 interval이라고 불리는 숫자 구간에 포함되는 연속적인 집합일 때는 Continuous Random Variable이라 부른다. -> 다음 글에서 다룰 내용!
9️⃣ Probability Mass Function (확률 질량 함수, PMF) 개념과 주요 Discrete RV 살펴보기
임의의 Discrete Random Variable에 대한 확률을 Probability Mass Function(확률 질량 함수, PMF)을 통해 구할 수 있다.
다시 말해, sample Space 내에 있는 각각의 outcome들에 대해 특정한 확률을 부여한 함수라고 생각하면 된다.
이 글 챕터 2️⃣에서 다뤘던 Axioms of Probability (확률 공리)의 내용이 Probability Mass Function에도 동일하게 적용된다.
- 임의의 x에 대해서 PMF가 가질 수 있는 확률은 0 이상이다.
- Sample space의 모든 outcome이 가질 수 있는 PMF probability 값의 합은 1이다.
- 임의의 event, B에 속하는 개별 outcome들이 일어날 PMF probability의 합은, 해당 event B의 PMF probability 전체 값을 나타낸다.

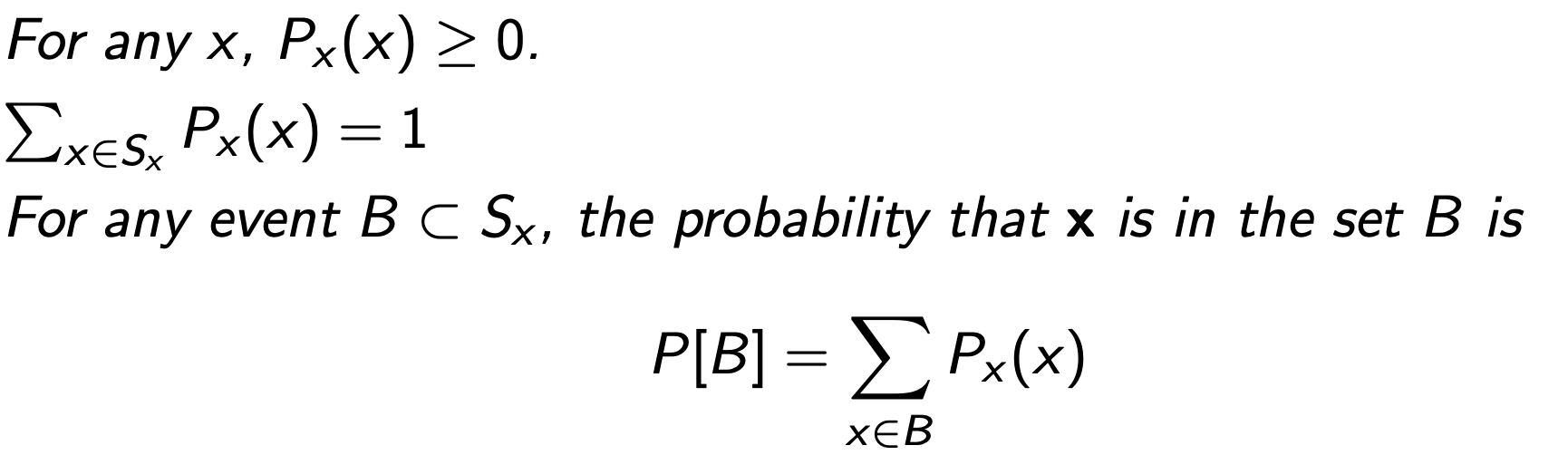

지금부터는 자주 쓰이는 특정한 Discrete RV에 대해 살펴보겠다.
✔️ Bernoulli RV
Bernoulli(p)의 형태로 표시한다.
PMF의 x가 0일 때와 1일 때 2가지 경우만 있으며, x가 1일 때는 p, 0일 때는 전체 확률 1-p를 갖는 간단한 RV이다. 두 가지 경우를 가지는 실험에 대해서 적용하기 적합한 Random Variable이다. (동전의 앞면과 뒷면, 주사위 짝수와 홀수 등)
Bernoulli의 PMF와 예시로, Bernoulli(0.2)일 때의 그래프는 아래와 같이 나타낼 수 있겠다.


✔️ Geometric RV
geometric(p)의 형태로 표시한다.
geometric RV의 핵심은 원하는 경우가 나올 때까지 Bernoulli RV를 가지는 실험을 실행했을 때의 확률값을 도출하는 것이다.
이게 무슨 말인지 이해하기 위해 예시를 하나 들어보겠다.
만약 주머니 안에 흰 공 1개와 검은 공 4개가 있고, 흰 공이 나올 때까지 반복해서 뽑는 실험이 있다고 치자. (뽑은 공은 다시 집어넣는다고 가정한다.) 흰 공이 나올 확률은 0.2(Bernoulli x값이 1인 셈), 검은 공이 나올 확률은 0.8(Bernoulli x값이 0인 셈)이겠다.
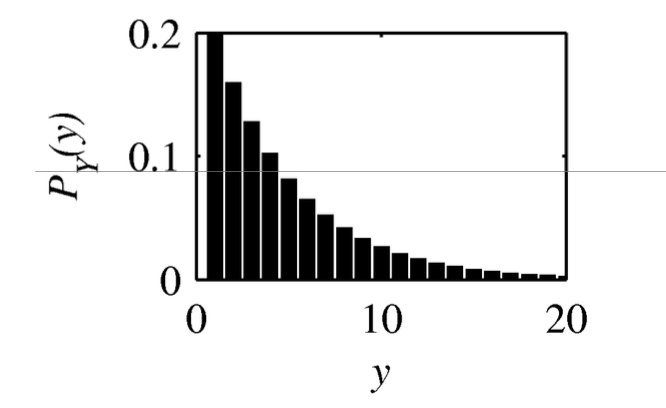
이때 첫 번째에 흰 공이 나올 확률은 0.2, 두번째에 흰공이 나올 확률은 0.8x0.2, 세번째에 흰공이 나올 확률은 0.8x0.8x0.2... 이런 식으로 쭉 나아가게 될 텐데, 이 확률값을 그래프로 표현하면 아래 오른쪽 모양과 같이 나오게 될 것이다.
첫 번째 실험에서 실험의 반복 횟수를 늘릴수록 확률은 떨어지는 형태가 Geometric RV의 확률이다.

✔️ Binomial RV
binomial(n, p)의 형태로 표시한다.
위의 Geometric RV 경우와는 다르게 이번에는 실험의 반복 횟수도 n으로 제시된다.
n번 반복 실험했을 때, 원하는 경우가 x번 나올 확률을 나타내는 것이 Binomial RV이다.
어디서 많이 본 것 같은데, 맞다. 위에서 배운 독립 시행의 확률, 이항분포의 내용과 일맥상통하는 개념이다.


✔️ Pascal RV
pascal(k, p)의 형태로 표시한다.
Pascal RV는 Geometric RV와 Binomial RV의 내용을 섞어놓은 듯하다.
실험을 정해진 횟수만큼 수행할 건데, 무작정 횟수가 정해진 것이 아니라 k번 원하는 경우가 나올 때까지 실험을 반복할 거다.
geometric에서 설명했던 공 예시를 들어서 설명해 보겠다.
흰 공이 3번 나올 때까지 실험을 한다고 했을 때,
실험 횟수 x가 4인 경우에는 3번까지는 흰 공 2번, 검은 공 1번이 나오고, 마지막 4번째 실험에서 반드시 흰 공이 나와야 할 것이다.
x가 5인 경우에는 4번까지는 흰 공 3번, 검은 공 1번이 나오고, 마지막 5번째 실험에서는 반드시 흰 공이 나와야 할 것이다.
이와 같이 최종 실험 횟수에 나와야 하는 경우는 무조건 정해져 있고, 그전까지는 Binomial RV와 같이 확률을 구해주는 것이 Pascal RV의 내용이다.

✔️ Discrete Uniform RV
discrete uniform(k, l)의 형태로 표시한다.
모든 outcome들이 동일한 확률로 분포되어 있는 경우를 나타내며, l은 실험의 최댓값 k는 실험의 최솟값이 들어가는 부분이다.
만약 uniform(1, 6)이라고 했을 때, 각각의 확률은 1 / 6-1+1 = 1/6으로 아래 오른쪽 그래프와 같이 표현해 줄 수 있겠다.


✔️ Poisson RV
poisson(α)의 형태로 표시한다.
Poisson RV는 시간과 사건의 발생횟수의 평균에 관한 정보를 알고 있을 때, 특정 시간동안 사건이 몇 번 발생할 것인가에 대한 확률 정보를 나타내는 랜덤변수이다.
Poisson이 어느 경우에 쓰이는지 예시를 들어보겠다.
어느 웹사이트의 방문자수가 Poisson RV를 따른다고 하고, 해당 사이트는 평균 1분당 120명의 방문자가 방문한다고 할 때,
1초동안 방문자가 x번 올 확률을 Poisson RV를 통해 구할 수 있게 된다.
α값은 문제에서 주어진 평균 발생횟수를 원하는 시간에 맞추어 적용시키면 되니까, 이 문제의 경우 α = 120 x (1/60)=2와 같이 구할 수 있겠다.

1️⃣0️⃣ Cumulative Distribution Function (누적 확률 분포 함수, CDF)
Discrete Random Variable에 대한 확률을 표현해주는 것이 위에서 배운 PMF 말고도 하나 더 존재하는데, 이를 Cumulative Distribution Function(누적 확률 분포 함수, CDF)라고 부른다.
CDF는 임의의 Random Variable x가 x 이하일 확률을 구하는 함수이다.
PMF 확률값을 누적하는 확률값이라 생각하면 편하며,
그렇기에 PMF와 CDF는 서로 밀접하게 연관되어 있어 서로가 서로를 보고 구할 수 있게 된다.

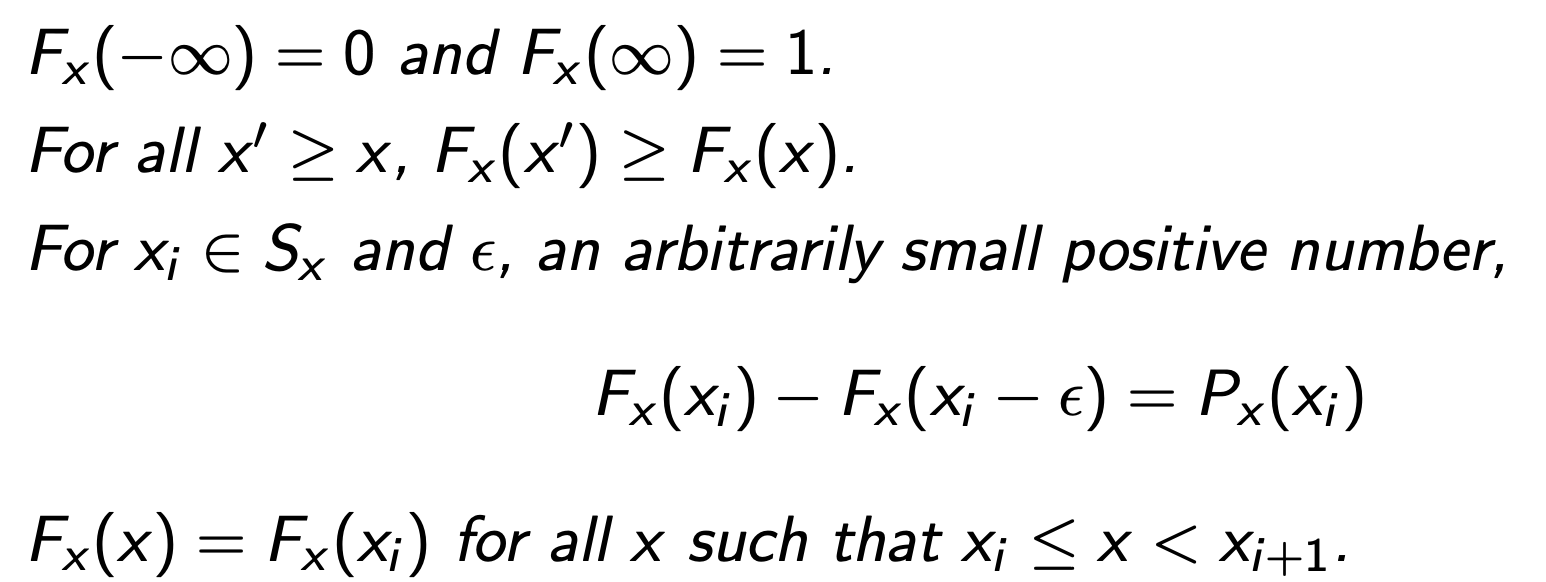
CDF의 기본 성질에 대해서도 알아보자.
총 4가지의 성질이고, 이를 통해 CDF가 어떤 식으로 그려질지를 어느 정도 유추해 볼 수 있겠다.
- CDF는 0에서 시작해서 최대 1로 끝나는 함수이다. -> PMF의 성질 (1), (2)에 대한 영향
- CDF는 non-decreasing function이다. -> 확률값이 계속 누적되는 영향
- 확률값이 존재하는 특정한 xi 지점에서 CDF는 계단과 같은 불연속이 나타나며, 그 계단의 높이는 xi일 때의 PMF값과 같다.
- 불연속이 나타나기 전까지 CDF 그래프는 수평선을 나타낸다.


오른쪽에 보이는 또 다른 성질도 있다.
다소 복잡해 보이지만, CDF의 높이 차이를 이용해서 PMF의 확률을 바로 구할 수 있는 비교적 간단한 이론이며,
a와 b 사이에 있는 부등호에만 주의를 기울이기 바란다.
1️⃣1️⃣ Averages and Expected Value
확률론에서 사용하는 Average의 개념은 총 3가지 종류가 있다.
- Mean : 우리가 흔히 사용하는 평균의 개념, 전체 숫자의 합을 개수로 나눈 것
- Median : 중앙값을 의미, number가 수치대로 정렬되어 있을 때 딱 가운데에 위치한 값 (outcome이 홀수이면 1개지만, 짝수일 경우 2개를 갖는다.)
- Mode : 최빈값을 의미, collection 안에서 가장 빈번하게 있는 값 (가장 많이 있는 값)
위의 3가지 Average들은 실험 관찰 결과의 집합을 설명할 때 사용되는 값이었다면,
실험의 확률 모델을 설명할 때 사용하는 값은 지금부터 배우게 될 Expected Value (기댓값, E[x], μx와 같이 표현)이다.
각 사건이 벌어졌을 때의 이득(x)과 해당 사건이 벌어질 확률(PMF)을 곱한 것을 전체 사건에 대해 합한 값의 형태로 구해주는데,
말이 어려워서 그렇지 그냥 간단하게 말했을 때 모든 경우에 대해 어떤 확률적 사건들의 평균과 같은 의미라고 생각하면 된다.
예시를 들어보겠다.
x=0일 때 1/4, x=1일 때 1/2, x=2일 때 1/4, otherwise 경우에 대해 확률이 0인 PMF가 있다고 했을 때,
이 Random Variable에 대한 Expected Value(E[x], μx)는 0*1/4 + 1*1/2 + 2*1/4의 식으로 구해줄 수 있다는 것이다.


그럼 위에서 배웠던 주요 Discrete Random Variable에 대해서도 기대값을 각각 정리해볼 수도 있겠다.
✔️ 주요 Discrete RV에 대한 Expected Value 정리
- Bernoulli(p) : E[x] = p
- geometric(p) : E[x] = 1/p
- binomial(n, p) : E[x] = np
- pascal(k, p) : E[x] = k/p
- discrete uniform(k, l) : E[x] = (k+l) / 2
- poisson(α) : E[x] = α
1️⃣2️⃣ Functions of a Random Variable
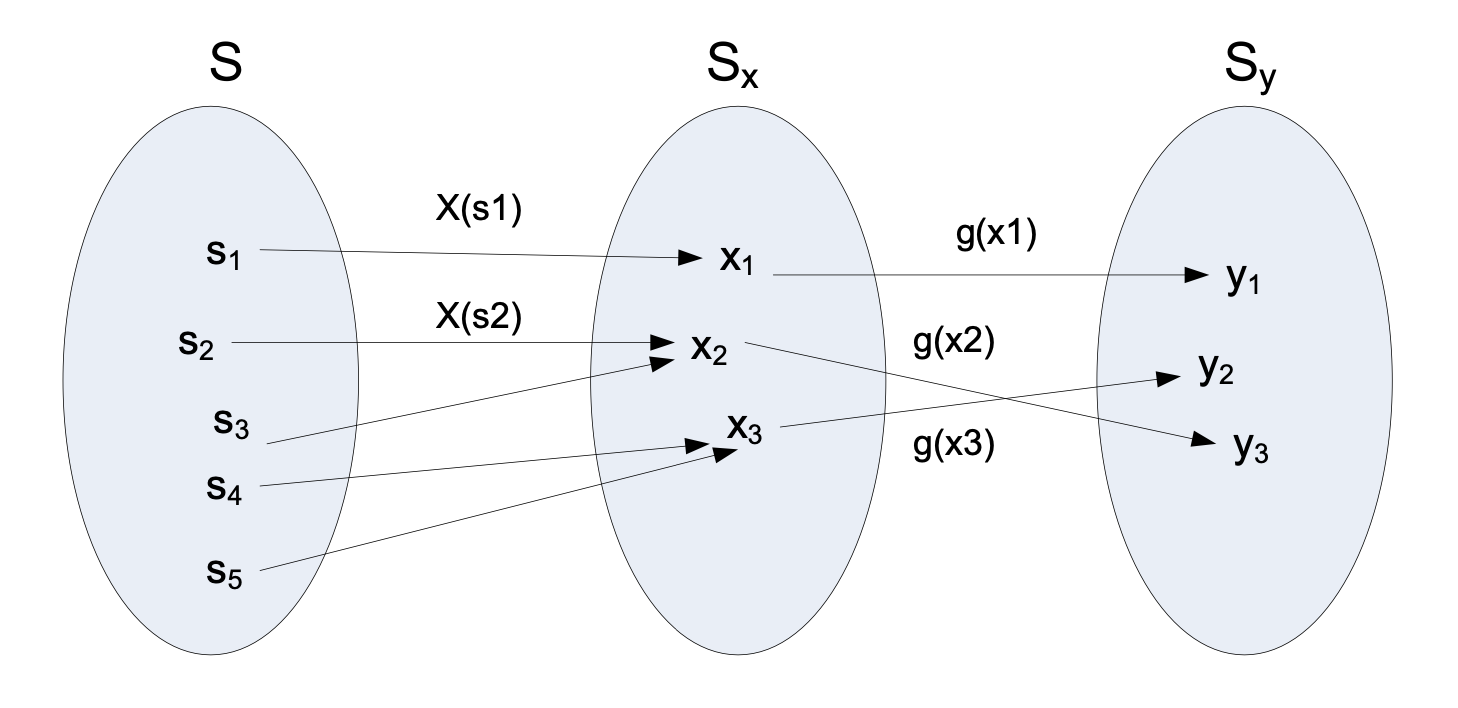
임의의 Random Variable x가 주어지고 실수함수 g(x)가 주어진다고 했을 때, Random Variable x를 실수함수 g(x)에 넣은 값, g(x)를 우리는 Function of Random Variable이라고 부른다.
표기는 y = g(x)와 같이 사용할 것이며, 함수를 통해 유도되는 Random Variable y 각각의 sample value y는 다른 Random Variable x 각각의 sample value x의 수학 함수 g(x)라고 설명할 수 있겠다.
= 쉽게 말해, 랜덤 변수 x를 다시 랜덤 변수 y 안에 넣는다고 생각하면 되겠다.
그러기에 Function of Random Variable y가 가지는 확률 PMF는 y에 대응되는 Random Variable x의 PMF 값들의 합으로 구할 수 있는 것이다.

확률이 주어졌으니, 위에서 배운 대로 Function of Random Variable y에 대한 기댓값도 구해볼 수 있겠다.
Expected Value E[y]는 sample space에 속하는 x에 대해 g(x)와 x의 PMF 값을 곱한 값들의 전체 합으로 구할 수 있다.
이 외에도 2개의 중요한 Expected Value와 관련된 공식(하나는 RV에서 기댓값을 뺀 값의 기댓값은 0, 또 다른 하나는 선형 변환과 관련있는 공식)이 나오니 아래 손글씨 정리를 참조해보자!


1️⃣3️⃣ Variance and Standard Deviation
우리가 앞에서 배웠던 Average의 개념으로는 Random Variable의 전형적인 값을 알 수 있었다. (Mean이든, Median이든, Mode든, Expected Value든)
다만, 여기에는 치명적인 단점이 존재하는데, 값들의 경향성을 알 수 없다는 것이다.
경향성은 중심으로부터 얼마나 퍼져 있는 Random Variable인가를 나타내는 척도 정도로 이해하면 된다.
이를 나타내는 수치가 고등학교에서 이미 배워본 적이 있는 분산(Variance)과 표준편차(Standard Deviation)이다.
Variance는 각각의 outcome과 평균의 차이를 제곱한 것들의 평균을 구한 값으로 구해주고, 여기에 루트를 취해주면 Standard Deviation이 된다.


다만, outcome들이 무수히 많은 경우에 대해 위와 같이 outcome 각각을 평균과의 차이를 구하고, 이를 제곱해 일일이 더해주기에는 너무 비효율적일 것이라 생각이 든다.
그래서 나온 공식이 아래 (1) 공식이다.
Random Variable 각각을 제곱한 값들의 평균과 Random Variable의 Expected Value를 제곱한 값의 차로 Variance를 구하는 방식이다.
(2) 공식 같은 경우는 Random Variable에 대해 곱해주는 경우에 대해 제곱만큼 분산이 늘어난다는 내용이다.
상식적으로 생각해 봐도, +와 -로 퍼지게 될 모양에서 곱해주면 제곱만큼 더 퍼지게 될 것이고, 더해주는 값에 대해서는 Average 값에 대해서만 영향이 생길 뿐 퍼져 있는 정도를 구하는 Variance에는 영향을 미치지 못할 것이란 걸 이해할 수 있다.
공식이 유도되는 과정은 마찬가지로 아래 풀이를 참조하자.


'Developer Basis' 카테고리의 다른 글
| [GitHub] 코드 리뷰 문화 - 토스터 iOS팀이 코드 스타일과 구성을 깔끔하게 유지할 수 있는 이유 (0) | 2024.03.26 |
|---|---|
| [Xcode] Xcode 커스텀하는 두 가지 방법 (Code Theme, App Icon) (0) | 2023.12.03 |
| [ML] 내가 머신러닝 진짜 알기 쉽게 정리해서 올려줄게 (23.10.19.ver) (1) | 2023.10.13 |
| [Calculus] Gradient Descent를 이해하기 위한 Vector Calculus 총정리 (1) | 2023.10.06 |
| [Probability and Random Variables] 머신러닝을 위한 확률이론 총정리 (1): Probability, Experiment Part (1) | 2023.10.02 |
